RANDN Gaussian (Normal) Random Number Generator
Section: Random Number Generation
Usage
Creates an array of pseudo-random numbers of the specified size. The numbers are normally distributed with zero mean and a unit standard deviation (i.e.,mu = 0, sigma = 1).
Two seperate syntaxes are possible. The first syntax specifies the array
dimensions as a sequence of scalar dimensions:
y = randn(d1,d2,...,dn).
The resulting array has the given dimensions, and is filled with
random numbers. The type of y is double, a 64-bit floating
point array. To get arrays of other types, use the typecast
functions.
The second syntax specifies the array dimensions as a vector,
where each element in the vector specifies a dimension length:
y = randn([d1,d2,...,dn]).
This syntax is more convenient for calling randn using a
variable for the argument.
Finally, randn supports two additional forms that allow
you to manipulate the state of the random number generator.
The first retrieves the state
y = randn('state')
which is a 625 length integer vector. The second form sets the state
randn('state',y)
or alternately, you can reset the random number generator with
randn('state',0)
Function Internals
Recall that the probability density function (PDF) of a normal random variable is
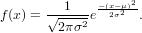
The Gaussian random numbers are generated from pairs of uniform random numbers using a transformation technique.
Example
The following example demonstrates an example of using the first form of therandn function.
--> randn(2,2,2) ans = (:,:,1) = -1.7375 -0.5664 -0.2634 -1.0112 (:,:,2) = -0.4020 0.0557 -1.8966 0.2098
The second example demonstrates the second form of the randn function.
--> randn([2,2,2])
ans =
(:,:,1) =
-0.7183 1.9415
0.1010 -1.1747
(:,:,2) =
0.3048 3.1685
-1.4185 -0.6130
In the next example, we create a large array of 10000 normally distributed pseudo-random numbers. We then shift the mean to 10, and the variance to 5. We then numerically calculate the mean and variance using mean and var, respectively.
--> x = 10+sqrt(5)*randn(1,10000);
--> mean(x)
ans =
10.0135
--> var(x)
ans =
4.9458
Now, we use the state manipulation functions of randn to exactly reproduce
a random sequence. Note that unlike using seed, we can exactly control where
the random number generator starts by saving the state.
--> randn('state',0) % restores us to startup conditions
--> a = randn(1,3) % random sequence 1
a =
-0.0362 -0.1404 0.6934
--> b = randn('state'); % capture the state vector
--> c = randn(1,3) % random sequence 2
c =
0.5998 0.7086 -0.9394
--> randn('state',b); % restart the random generator so...
--> c = randn(1,3) % we get random sequence 2 again
c =
0.5998 0.7086 -0.9394
