RANDGAMMA Generate Gamma-Distributed Random Variable
Section: Random Number Generation
Usage
Generates random variables with a gamma distribution. The general syntax for its use isy = randgamma(a,r),
where a and r are vectors describing the parameters of the
gamma distribution. Roughly speaking, if a is the mean time between
changes of a Poisson random process, and we wait for the r change,
the resulting wait time is Gamma distributed with parameters a
and r.
Function Internals
The Gamma distribution arises in Poisson random processes. It represents the waiting time to the occurance of ther-th event in a process with
mean time a between events. The probability distribution of a Gamma
random variable is
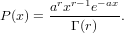
Note also that for integer values of r that a Gamma random variable
is effectively the sum of r exponential random variables with parameter
a.
Example
Here we use therandgamma function to generate Gamma-distributed
random variables, and then generate them again using the randexp
function.
--> randgamma(1,15*ones(1,9)) ans = Columns 1 to 8 22.7804 11.5514 16.8537 12.7457 16.2303 10.7442 19.3942 16.3611 Columns 9 to 9 17.4772 --> sum(randexp(ones(15,9))) ans = Columns 1 to 8 14.6404 15.1860 13.3147 11.4380 7.2307 10.8225 14.5271 12.4631 Columns 9 to 9 11.8753
