TIMES Matrix Multiply Operator

Section: Mathematical Operators

Usage

Multiplies two numerical arrays. This operator is really a combination of three operators, all of which have the same general syntax: 
  y = a * b

where a and b are arrays of numerical type. The result y depends on which of the following three situations applies to the arguments a and b:

  1. a is a scalar, b is an arbitrary n-dimensional numerical array, in which case the output is the element-wise product of b with the scalar a.
  2. b is a scalar, a is an arbitrary n-dimensional numerical array, in which case the output is the element-wise product of a with the scalar b.
  3. a,b are conformant matrices, i.e., a is of size M x K, and b is of size K x N, in which case the output is of size M x N and is the matrix product of a, and b.
Matrix multiplication is only defined for matrices of type double and single.

Function Internals

There are three formulae for the times operator. For the first form

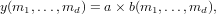
and the second form

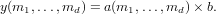
In the third form, the output is the matrix product of the arguments

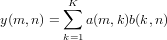
Examples

Here are some examples of using the matrix multiplication operator. First, the scalar examples (types 1 and 2 from the list above): 
--> a = [1,3,4;0,2,1]

a = 
 1 3 4 
 0 2 1 

--> b = a * 2

b = 
 2 6 8 
 0 4 2

The matrix form, where the first argument is 2 x 3, and the second argument is 3 x 1, so that the product is size 2 x 1. 

--> a = [1,2,0;4,2,3]

a = 
 1 2 0 
 4 2 3 

--> b = [5;3;1]

b = 
 5 
 3 
 1 

--> c = a*b

c = 
 11 
 29

Note that the output is double precision.