LEFTDIVIDE Matrix Equation Solver/Divide Operator

Section: Mathematical Operators

Usage

The divide operator \ is really a combination of three operators, all of which have the same general syntax: 
  Y = A \ B

where A and B are arrays of numerical type. The result Y depends on which of the following three situations applies to the arguments A and B:

  1. A is a scalar, B is an arbitrary n-dimensional numerical array, in which case the output is each element of B divided by the scalar A.
  2. A,B are matrices with the same number of rows, i.e., A is of size M x K, and B is of size M x L, in which case the output is of size K x L.
The output follows the standard type promotion rules, although in the first two cases, if A and B are integers, the output is an integer also, while in the third case if A and B are integers, the output is of type double. A few additional words about the third version, in which A and B are matrices. Very loosely speaking, Y is the matrix that satisfies A * Y = B. In cases where such a matrix exists. If such a matrix does not exist, then a matrix Y is returned that approximates A * Y \approx B.

Function Internals

There are three formulae for the times operator. For the first form

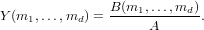
In the second form, the calculation of the output depends on the size of A. Because each column of B is treated independantly, we can rewrite the equation A Y = B as

where y_i are the columns of Y, and b_i are the columns of the matrix B. If A is a square matrix, then the LAPACK routine *gesvx (where the * is replaced with sdcz depending on the type of the arguments) is used, which uses an LU decomposition of A to solve the sequence of equations sequentially. If A is singular, then a warning is emitted. On the other hand, if A is rectangular, then the LAPACK routine *gelsy is used. Note that these routines are designed to work with matrices A that are full rank - either full column rank or full row rank. If A fails to satisfy this assumption, a warning is emitted. If A has full column rank (and thus necessarily has more rows than columns), then theoretically, this operator finds the columns y_i that satisfy:

and each column is thus the Least Squares solution of A y = b_i. On the other hand, if A has full row rank (and thus necessarily has more columns than rows), then theoretically, this operator finds the columns y_i that satisfy

and each column is thus the Minimum Norm vector y_i that satisfies A y_i = b_i. In the event that the matrix A is neither full row rank nor full column rank, a solution is returned, that is the minimum norm least squares solution. The solution is computed using an orthogonal factorization technique that is documented in the LAPACK User's Guide (see the References section for details).

Examples

Here are some simple examples of the divide operator. We start with a simple example of a full rank, square matrix: 
--> A = [1,1;0,1]

A = 
 1 1 
 0 1

Suppose we wish to solve

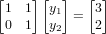
(which by inspection has the solution y_1 = 1, y_2 = 2). Thus we compute: 

--> B = [3;2]

B = 
 3 
 2 

--> Y = A\B

Y = 
 1 
 2

Suppose we wish to solve a trivial Least Squares (LS) problem. We want to find a simple scaling of the vector [1;1] that is closest to the point [2,1]. This is equivalent to solving

in a least squares sense. For fun, we can calculate the solution using calculus by hand. The error we wish to minimize is

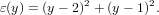
Taking a derivative with respect to y, and setting to zero (which we must have for an extrema when y is unconstrained)

which we can simplify to 4y = 6 or y = 3/2 (we must, technically, check to make sure this is a minimum, and not a maximum or an inflection point). Here is the same calculation performed using FreeMat: 

--> A = [1;1]

A = 
 1 
 1 

--> B = [2;1]

B = 
 2 
 1 

--> A\B

ans = 
    1.5000

which is the same solution.