PINV Moore-Penrose Pseudoinverse
Section: Array Generation and Manipulations
Usage
Calculates the Moore-Penrose pseudoinverse of a matrix. The general syntax for its use isy = pinv(A,tol)
or for a default specification of the tolerance tol,
y = pinv(A)
For any m x n matrix A, the Moore-Penrose pseudoinverse
is the unique n x m matrix B that satisfies the following
four conditions
-
A B A = A -
B A B = B -
(A B)' = A B -
(B A)' = B A
B y is the minimum norm, least squares
solution to A x = y. The Moore-Penrose pseudoinverse is computed
from the singular value decomposition of A, with singular values
smaller than tol being treated as zeros. If tol is not specified
then it is chosen as
tol = max(size(A)) * norm(A) * teps(A).
Function Internals
The calculation of the MP pseudo-inverse is almost trivial once the svd of the matrix is available. First, for a real, diagonal matrix with positive entries, the pseudo-inverse is simply
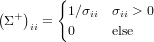
One can quickly verify that this choice of matrix satisfies the
four properties of the pseudoinverse. Then, the pseudoinverse
of a general matrix A = U S V' is defined as
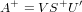
and again, using the facts that U' U = I and V V' = I, one
can quickly verify that this choice of pseudoinverse satisfies the
four defining properties of the MP pseudoinverse. Note that in
practice, the diagonal pseudoinverse S^{+} is computed with
a threshold (the tol argument to pinv) so that singular
values smaller than tol are treated like zeros.
Examples
Consider a simple1 x 2 matrix example, and note the various
Moore-Penrose conditions:
--> A = float(rand(1,2))
A =
0.9526 0.4847
--> B = pinv(A)
B =
0.8338
0.4243
--> A*B*A
ans =
0.9526 0.4847
--> B*A*B
ans =
0.8338
0.4243
--> A*B
ans =
1.0000
--> B*A
ans =
0.7943 0.4042
0.4042 0.2057
To demonstrate that pinv returns the least squares solution,
consider the following very simple case
--> A = float([1;1;1;1]) A = 1 1 1 1
The least squares solution to A x = b is just x = mean(b),
and computing the pinv of A demonstrates this
--> pinv(A)
ans =
0.2500 0.2500 0.2500 0.2500
Similarly, we can demonstrate the minimum norm solution with the following simple case
--> A = float([1,1]) A = 1 1
The solutions of A x = 5 are those x_1 and x_2 such that
x_1 + x_2 = 5. The norm of x is x_1^ + x_2^2, which is
x_1^2 + (5-x_1)^2, which is minimized for x_1 = x_2 = 2.5:
--> pinv(A) * 5.0
ans =
2.5000
2.5000
