DET Determinant of a Matrix
Section: Array Generation and Manipulations
Usage
Calculates the determinant of a matrix. Note that for all but very small problems, the determinant is not particularly useful. The condition numbercond gives a more reasonable estimate as
to the suitability of a matrix for inversion than comparing det(A)
to zero. In any case, the syntax for its use is
y = det(A)
where A is a square matrix.
Function Internals
The determinant is calculated via theLU decomposition. Note that
the determinant of a product of matrices is the product of the
determinants. Then, we have that

where L is lower triangular with 1s on the main diagonal, U is
upper triangular, and P is a row-permutation matrix. Taking the
determinant of both sides yields
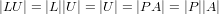
where we have used the fact that the determinant of L is 1. The
determinant of P (which is a row exchange matrix) is either 1 or
-1.
Example
Here we assemble a random matrix and compute its determinant--> A = rand(5); --> det(A) ans = -0.1160
Then, we exchange two rows of A to demonstrate how the determinant
changes sign (but the magnitude is the same)
--> B = A([2,1,3,4,5],:);
--> det(B)
ans =
0.1160
