SVD Singular Value Decomposition of a Matrix
Section: Transforms/Decompositions
Usage
Computes the singular value decomposition (SVD) of a matrix. Thesvd function has three forms. The first returns only the singular
values of the matrix:
s = svd(A)
The second form returns both the singular values in a diagonal
matrix S, as well as the left and right eigenvectors.
[U,S,V] = svd(A)
The third form returns a more compact decomposition, with the left and right singular vectors corresponding to zero singular values being eliminated. The syntax is
[U,S,V] = svd(A,0)
Function Internals
Recall thatsigma_i is a singular value of an M x N
matrix A if there exists two vectors u_i, v_i where u_i is
of length M, and v_i is of length u_i and
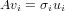
and generally
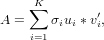
where K is the rank of A. In matrix form, the left singular
vectors u_i are stored in the matrix U as
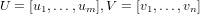
The matrix S is then of size M x N with the singular
values along the diagonal. The SVD is computed using the
LAPACK class of functions GESVD (Note that this has
changed. Previous versions of FreeMat used GESDD, which
yields a valid, but slightly different choice of the decomposition.
Starting in version 4, it was changed to GESVD to improve
compatibility.
Examples
Here is an example of a partial and complete singular value decomposition.
--> A = float(randn(2,3))
A =
-0.9542 1.2478 -0.2295
0.3075 1.0686 -0.4849
--> [U,S,V] = svd(A)
U =
-0.8410 -0.5411
-0.5411 0.8410
S =
1.8058 0 0
0 0.8549 0
V =
0.3522 0.9064 0.2331
-0.9013 0.2614 0.3454
0.2521 -0.3317 0.9091
--> U*S*V'
ans =
-0.9542 1.2478 -0.2295
0.3075 1.0686 -0.4849
--> svd(A)
ans =
1.8058
0.8549
