CONV2 Matrix Convolution
Section: Signal Processing Functions
Usage
Theconv2 function performs a two-dimensional convolution of
matrix arguments. The syntax for its use is
Z = conv2(X,Y)
which performs the full 2-D convolution of X and Y. If the
input matrices are of size [xm,xn] and [ym,yn] respectively,
then the output is of size [xm+ym-1,xn+yn-1]. Another form is
Z = conv2(hcol,hrow,X)
where hcol and hrow are vectors. In this form, conv2
first convolves Y along the columns with hcol, and then
convolves Y along the rows with hrow. This is equivalent
to conv2(hcol(:)*hrow(:)',Y).
You can also provide an optional shape argument to conv2
via either
Z = conv2(X,Y,'shape')
Z = conv2(hcol,hrow,X,'shape')
where shape is one of the following strings
-
'full'- compute the full convolution result - this is the default if noshapeargument is provided. -
'same'- returns the central part of the result that is the same size asX. -
'valid'- returns the portion of the convolution that is computed without the zero-padded edges. In this situation,Zhas size[xm-ym+1,xn-yn+1]whenxm>=ymandxn>=yn. Otherwiseconv2returns an empty matrix.
Function Internals
The convolution is computed explicitly using the definition:
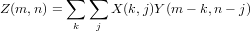
If the full output is requested, then m ranges over 0 <= m < xm+ym-1
and n ranges over 0 <= n < xn+yn-1. For the case where shape
is 'same', the output ranges over (ym-1)/2 <= m < xm + (ym-1)/2
and (yn-1)/2 <= n < xn + (yn-1)/2.
