MATRIXPOWER Matrix Power Operator
Section: Mathematical Operators
Usage
The power operator for scalars and square matrices. This operator is really a combination of two operators, both of which have the same general syntax:y = a ^ b
The exact action taken by this operator, and the size and type of the output,
depends on which of the two configurations of a and b is present:
-
ais a scalar,bis a square matrix -
ais a square matrix,bis a scalar
Function Internals
In the first case thata is a scalar, and b is a square matrix, the matrix power is defined in terms of the eigenvalue decomposition of b. Let b have the following eigen-decomposition (problems arise with non-symmetric matrices b, so let us assume that b is symmetric):

Then a raised to the power b is defined as

Similarly, if a is a square matrix, then a has the following eigen-decomposition (again, suppose a is symmetric):

Then a raised to the power b is defined as
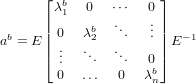
Examples
We first define a simple2 x 2 symmetric matrix
--> A = 1.5
A =
1.5000
--> B = [1,.2;.2,1]
B =
1.0000 0.2000
0.2000 1.0000
First, we raise B to the (scalar power) A:
--> C = B^A
C =
1.0150 0.2995
0.2995 1.0150
Next, we raise A to the matrix power B:
--> C = A^B
C =
1.5049 0.1218
0.1218 1.5049
