ATAN2 Inverse Trigonometric 4-Quadrant Arctangent Function
Section: Mathematical Functions
Usage
Computes theatan2 function for its argument. The general
syntax for its use is
z = atan2(y,x)
where x and y are n-dimensional arrays of numerical type.
Integer types are promoted to the double type prior to
calculation of the atan2 function. The size of the output depends
on the size of x and y. If x is a scalar, then z
is the same size as y, and if y is a scalar, then z
is the same size as x. The type of the output is equal to the type of
|y/x|.
Function Internals
The function is defined (for real values) to return an angle between-pi and pi. The signs of x and y
are used to find the correct quadrant for the solution. For complex
arguments, the two-argument arctangent is computed via
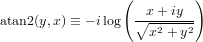
For real valued arguments x,y, the function is computed directly using
the standard C library's numerical atan2 function. For both
real and complex arguments x, note that generally
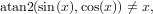
due to the periodicities of cos(x) and sin(x).
Example
The following code demonstates the difference between theatan2
function and the atan function over the range [-pi,pi].
--> x = linspace(-pi,pi); --> sx = sin(x); cx = cos(x); --> plot(x,atan(sx./cx),x,atan2(sx,cx))
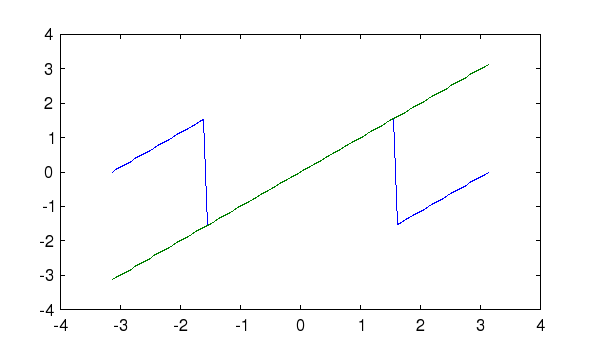
Note how the two-argument atan2 function (green line)
correctly ``unwraps'' the phase of the angle, while the atan
function (red line) wraps the angle to the interval [-\pi/2,\pi/2].
