FITFUN Fit a Function
Section: Optimization and Curve Fitting
Usage
Fitsn (non-linear) functions of m variables using least squares
and the Levenberg-Marquardt algorithm. The general syntax for its usage
is
[xopt,yopt] = fitfun(fcn,xinit,y,weights,tol,params...)
Where fcn is the name of the function to be fit, xinit is the
initial guess for the solution (required), y is the right hand side,
i.e., the vector y such that:
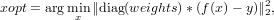
the output yopt is the function fcn evaluated at xopt.
The vector weights must be the same size as y, and contains the
relative weight to assign to an error in each output value. Generally,
the ith weight should reflect your confidence in the ith measurement.
The parameter tol is the tolerance used for convergence.
The function fcn must return a vector of the same size as y,
and params are passed to fcn after the argument x, i.e.,
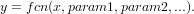
Note that both x and y (and the output of the function) must all
be real variables. Complex variables are not handled yet.
